직육면체 겉넓이 공식 완벽 정리: 예제와 함께 배우는 수학
직육면체는 수학에서 매우 기본적이고 중요한 도형 중 하나입니다. 일상생활에서 다양한 형태로 접할 수 있으며, 그 특성상 계산과 측정에 자주 사용됩니다. 이번 블로그 포스트에서는 직육면체의 겉넓이를 계산하는 공식을 자세히 살펴보고, 이해를 돕기 위해 예제와 함께 설명하겠습니다.

1. 직육면체란?
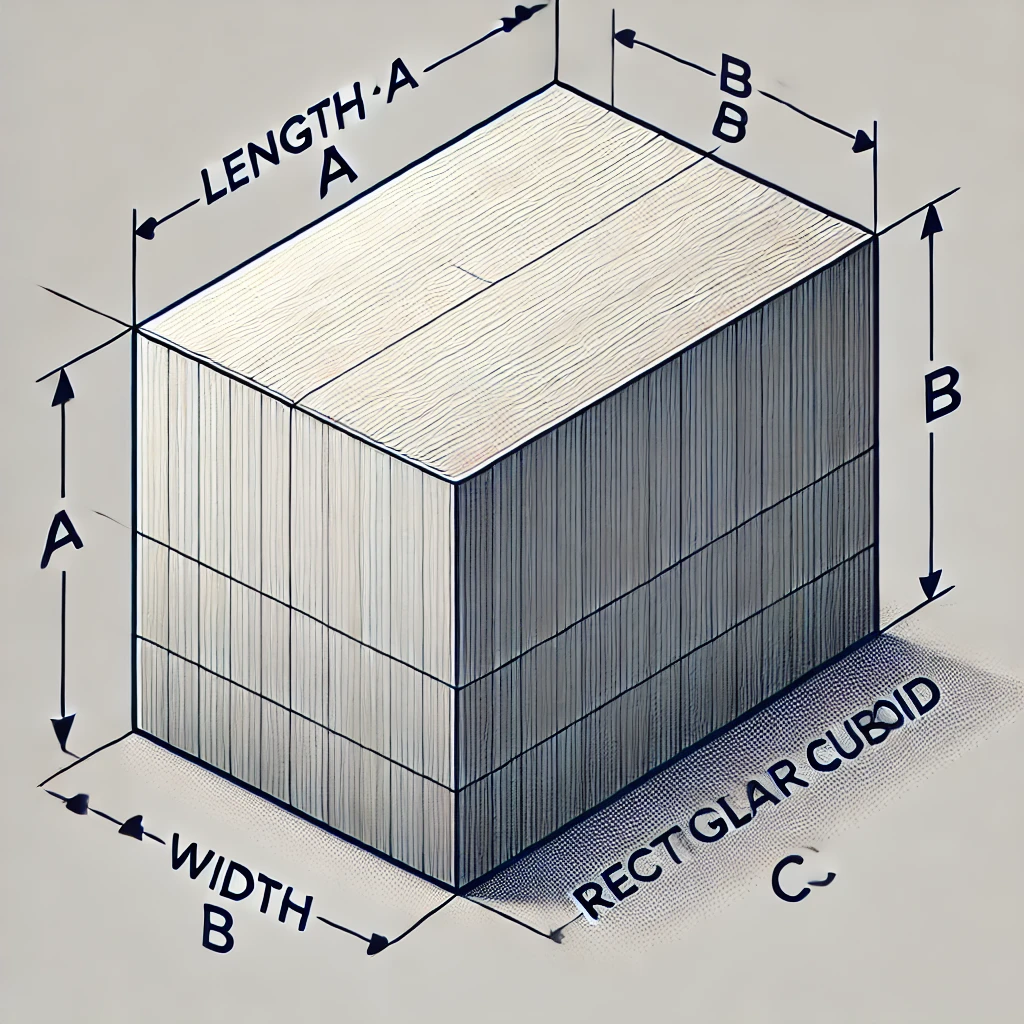
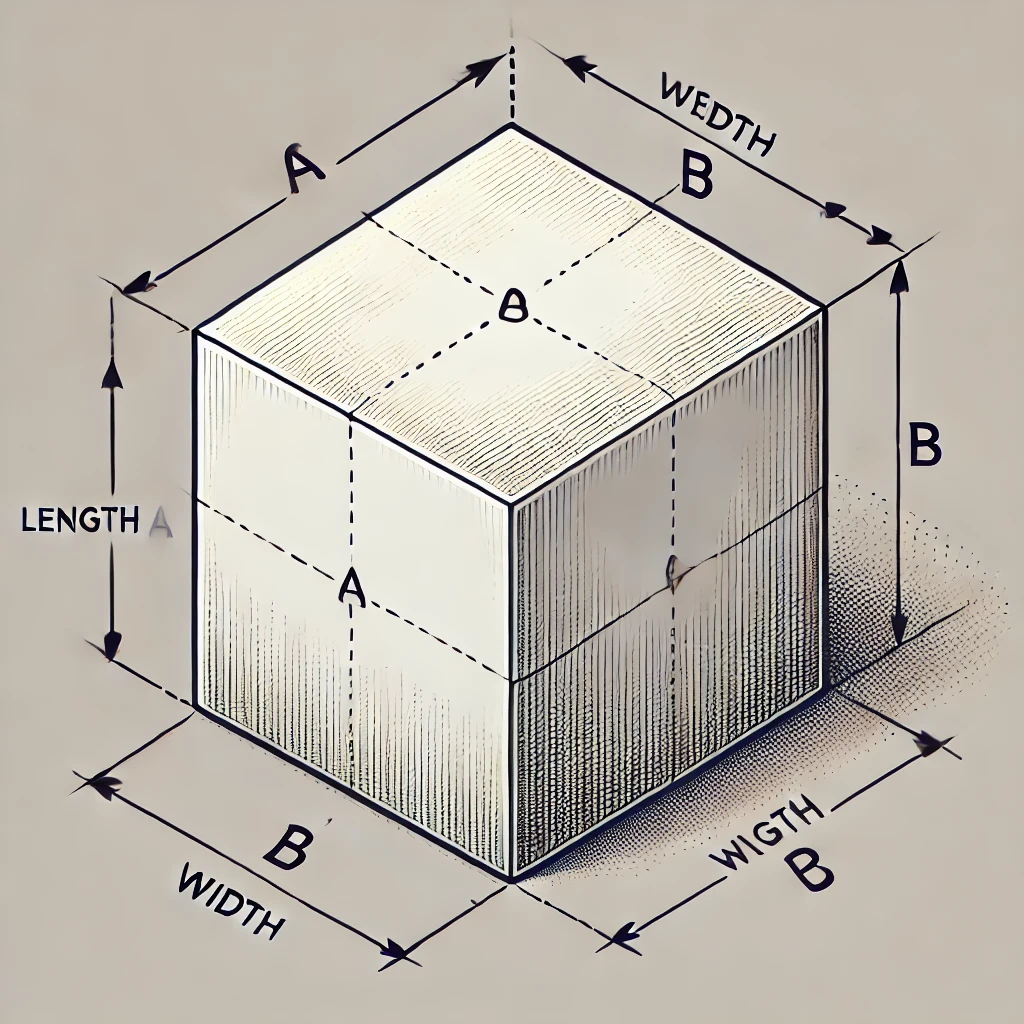
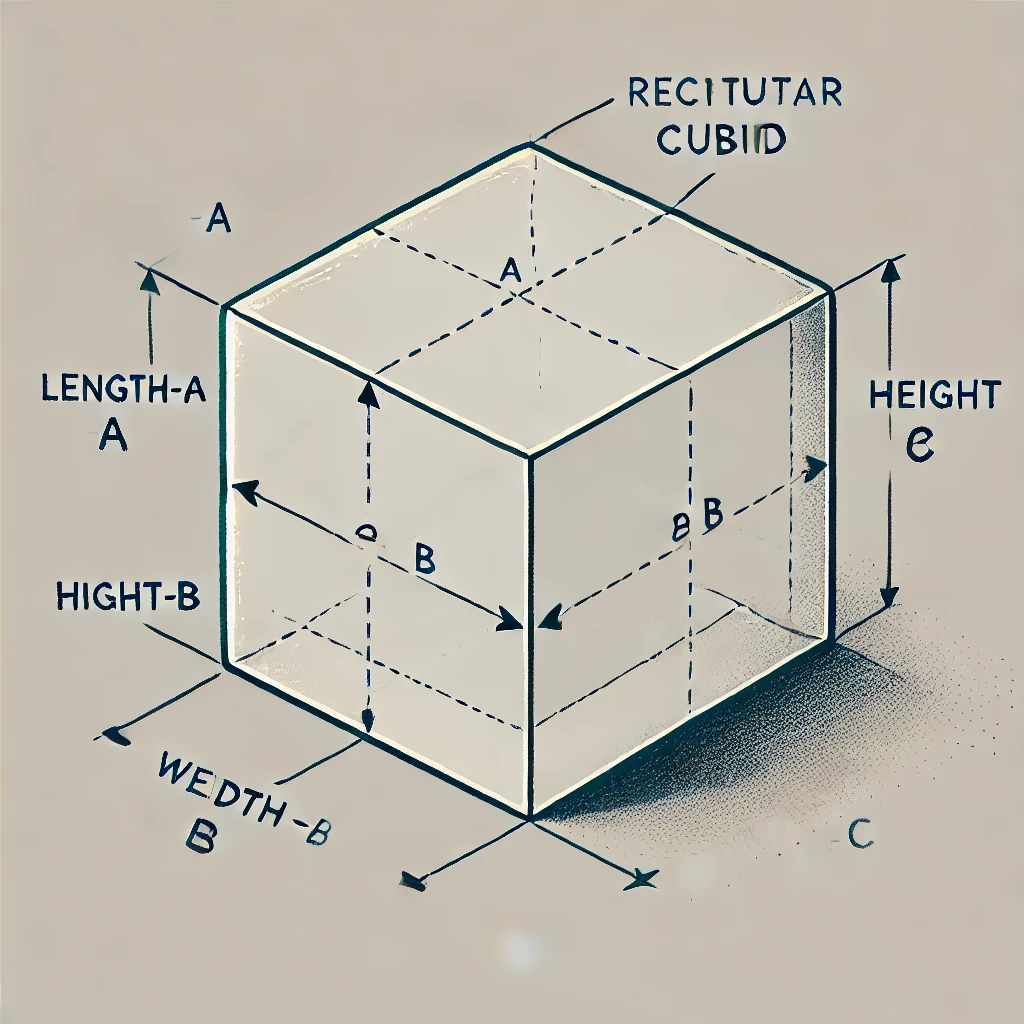
직육면체는 세 변이 서로 수직으로 만나는 여섯 개의 직사각형 면으로 이루어진 입체 도형입니다. 세 변의 길이를 각각 a, b, c라고 할 때, 직육면체는 다음과 같은 특징을 가집니다.
- 모서리의 수: 12개
- 면의 수: 6개
- 꼭짓점의 수: 8개
이러한 특징으로 인해 직육면체는 다양한 분야에서 활용됩니다.
2. 직육면체 겉넓이 공식
직육면체의 겉넓이는 그 표면적을 의미합니다. 직육면체의 여섯 개 면의 넓이를 모두 더하면 겉넓이를 구할 수 있습니다. 직육면체의 겉넓이 공식은 다음과 같습니다.
겉넓이=2(ab+bc+ca)
여기서,
- a: 직육면체의 길이
- b: 직육면체의 너비
- : 직육면체의 높이
이 공식을 이용하면 각 면의 넓이를 쉽게 계산하고, 더할 수 있습니다.
3. 예제와 함께 배우는 겉넓이 계산
예제 1
길이 a=cm, 너비 b=cm, 높이 c=cm인 직육면체의 겉넓이를 구해봅시다.
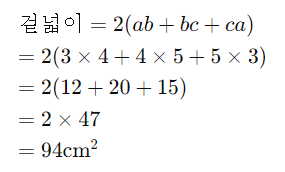
따라서, 이 직육면체의 겉넓이는 94제곱센티미터입니다.
예제 2
길이 a=m, 너비 b=m, 높이 c=m인 직육면체의 겉넓이를 구해봅시다.
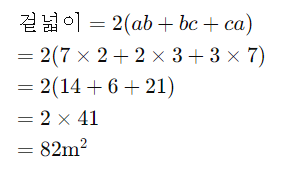
이 직육면체의 겉넓이는 82제곱미터입니다.
4. 직육면체 겉넓이 공식의 응용
직육면체의 겉넓이 계산은 일상생활에서 매우 유용하게 사용됩니다. 예를 들어, 선물 상자의 포장지 크기를 계산하거나, 건축 현장에서 벽지나 페인트의 양을 계산할 때 활용할 수 있습니다.
실생활 예제: 포장지 계산
길이 30cm, 너비 20cm, 높이 10cm인 선물 상자를 포장하려고 합니다. 필요한 포장지의 최소 크기를 계산해 봅시다.
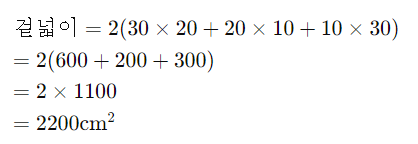
따라서, 최소한 2200제곱센티미터의 포장지가 필요합니다.
결론
직육면체의 겉넓이를 계산하는 공식은 매우 간단하지만, 그 응용 범위는 매우 넓습니다. 기본적인 수학 지식으로부터 출발하여 실생활에 유용한 정보를 제공하는 직육면체의 겉넓이 공식에 대해 충분히 이해하고 활용해보세요. 이제 여러분도 다양한 직육면체의 겉넓이를 쉽게 계산할 수 있을 것입니다.
'정보' 카테고리의 다른 글
| 교종과 선종의 차이: 불교의 두 갈래 (0) | 2024.09.14 |
|---|---|
| 시민 불복종의 사례와 철학적 배경 (0) | 2024.07.13 |
| 최소공배수 구하는법: 간단하고 쉽게 배우는 방법 (0) | 2024.07.09 |
| 비평문 예시: 문학 작품과 영화 분석 (0) | 2024.07.03 |
| 삼각함수의 실생활 활용 예시 8가지 (0) | 2024.05.31 |




댓글