삼각함수의 실생활 활용 예시 8가지
삼각함수는 수학에서 중요한 개념 중 하나로, 다양한 실생활에서 활용됩니다. 이 글에서는 삼각함수가 어떻게 우리의 일상 속에서 유용하게 사용되는지에 대해 설명합니다. 예를 들어, 건축, 엔지니어링, 천문학, 음악, 의료 분야 등에서 삼각함수의 응용 방법을 다룹니다. 또한, 삼각함수를 쉽게 이해하고 활용할 수 있는 방법을 소개하여 독자들이 삼각함수를 보다 친숙하게 느끼도록 합니다.

1. 삼각함수란 무엇인가?
삼각함수의 정의와 기본 개념
삼각함수는 각도의 크기를 이용해 삼각형의 변의 길이를 나타내는 함수입니다. 주로 사인(sin), 코사인(cos), 탄젠트(tan) 등의 함수가 있습니다. 삼각함수는 직각삼각형에서 각도와 변의 관계를 나타내는데, 이는 다양한 수학적 문제를 해결하는 데 필수적입니다.
삼각함수의 종류
삼각함수에는 사인, 코사인, 탄젠트 외에도 코시컨트(csc), 시컨트(sec), 코탄젠트(cot) 등이 있습니다. 각각의 함수는 직각삼각형의 특정한 변과 각도 사이의 비율을 나타내며, 이를 통해 다양한 계산이 가능합니다.
2. 삼각함수의 실생활 활용 예시
건축과 엔지니어링에서의 활용
건축과 엔지니어링 분야에서 삼각함수는 구조물의 높이, 각도, 거리 등을 계산하는 데 사용됩니다. 예를 들어, 빌딩의 높이를 측정하거나 다리의 각도를 설계하는 데 삼각함수를 활용할 수 있습니다.
건축과 토목 공학
삼각함수는 건축과 토목 공학에서 구조물의 설계와 분석에 널리 사용됩니다. 예를 들어, 다음과 같은 상황에서 삼각함수가 중요한 역할을 합니다:
- 건물의 높이와 거리 측정: 삼각함수를 이용해 건물의 높이를 정확하게 측정할 수 있습니다. 예를 들어, 건물 앞에서 일정 거리를 두고 측량기기로 각도를 측정한 후 삼각함수를 사용해 높이를 계산할 수 있습니다.
- 지붕의 경사 설계: 지붕의 경사를 결정할 때 삼각함수를 사용하여 눈, 비 등의 하중을 효율적으로 분산시키는 경사각을 설계합니다. 이는 건물의 구조적 안정성을 높이는 데 중요합니다.
- 다리와 교량 설계: 삼각함수는 다리의 아치 형태를 설계하고, 하중을 분산시키는 데 필수적입니다. 이를 통해 다리의 내구성을 향상시키고, 안전한 교량을 건설할 수 있습니다.

천문학에서의 활용
천문학에서는 별과 행성의 위치를 계산하는 데 삼각함수가 필수적입니다. 천체의 고도와 방위를 계산하여 정확한 위치를 파악하고, 이를 통해 천체 관측과 연구를 진행할 수 있습니다.
음악에서의 활용
음악에서는 소리의 파형 분석과 같은 분야에서 삼각함수가 사용됩니다. 사운드 엔지니어들은 삼각함수를 이용해 소리의 주파수와 파장을 분석하고, 이를 통해 음질을 조정하거나 음악을 믹싱할 수 있습니다.
의료 분야에서의 활용
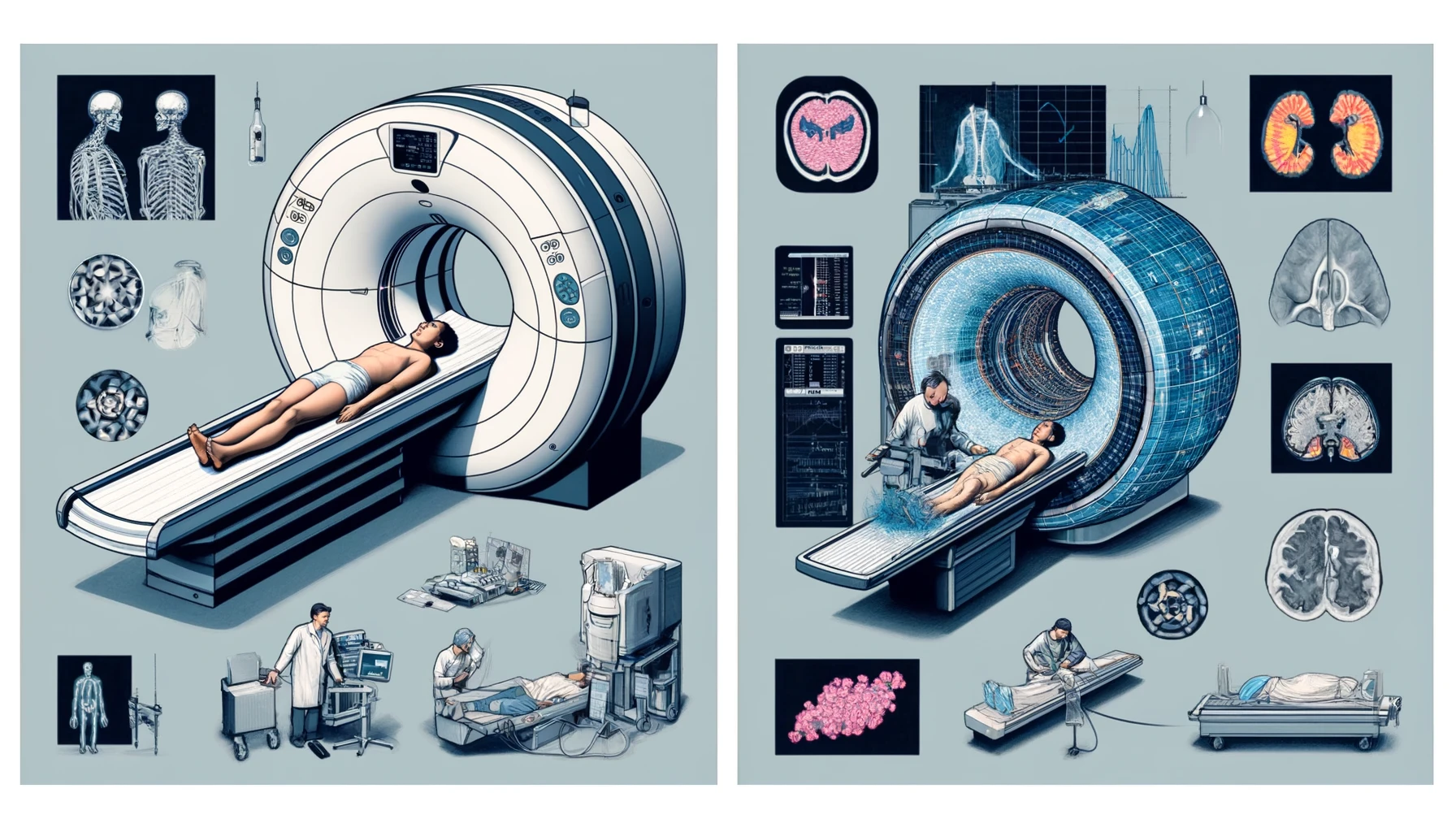
의료 분야에서는 MRI나 CT 스캔과 같은 이미지 처리 기술에 삼각함수가 사용됩니다. 이러한 기술들은 삼각함수를 이용해 인체 내부의 이미지를 정확하게 재구성하고 분석할 수 있습니다.
의료 영상
의료 영상 기술에서는 삼각함수를 이용해 인체 내부의 이미지를 생성하고 분석합니다. 특히, 다음과 같은 사례에서 삼각함수가 사용됩니다:
- CT 스캔: 다양한 각도에서 X선을 투과시켜 인체 단면 영상을 얻은 후, 삼각함수를 사용해 3D 이미지를 재구성합니다. 이를 통해 의사들은 종양, 골절 등 다양한 질병을 진단할 수 있습니다.
- MRI 스캔: 강한 자기장을 이용해 인체 내부의 이미지를 생성하며, 삼각함수를 사용해 정확한 단면도를 만듭니다. 이를 통해 뇌, 척수 등의 조직 상태를 정밀하게 분석합니다.
- 초음파: 초음파를 이용해 인체 내부를 촬영할 때, 반사된 신호의 각도와 시간을 분석하여 이미지를 생성하는 데 삼각함수를 활용합니다.
항공과 항해
항공기와 선박의 항로를 계획하고 실행하는 데 있어서 삼각함수는 필수적입니다. 다음과 같은 활용 사례가 있습니다:
- 비행 경로 계산: 비행기의 출발지와 도착지 사이의 최단 경로를 계산할 때 삼각함수를 사용합니다. 특히, 대원(大圓) 항법을 사용하여 지구의 곡면을 따라 비행 경로를 최적화합니다.
- 위도와 경도 계산: 항공기나 선박의 위치를 파악하기 위해 삼각함수를 이용해 위도와 경도를 계산합니다. 이는 정확한 위치 추적과 항로 수정에 매우 중요합니다.
- 항로 최적화: 연료 소비를 최소화하고, 비행 시간을 단축하기 위해 항공기와 선박의 항로를 삼각함수를 이용해 최적화합니다.

물리학과 엔지니어링
물리학과 엔지니어링 분야에서도 삼각함수는 다양한 응용을 가지고 있습니다. 몇 가지 구체적인 사례를 살펴보겠습니다:
- 파동 분석: 소리, 빛, 전자기파 등의 파동 현상을 설명하고 분석할 때 삼각함수를 사용합니다. 예를 들어, 소리의 주파수와 진폭을 분석하여 음향 설계를 최적화합니다.
- 진동 분석: 기계나 구조물의 진동을 분석할 때 삼각함수를 사용합니다. 이는 진동을 줄이고, 구조물의 안정성을 높이는 데 필수적입니다.
- 전기 회로 분석: 전기 회로에서 교류 전압과 전류의 위상 차이를 계산하고, 이를 통해 회로의 성능을 최적화합니다.
컴퓨터 그래픽스
컴퓨터 그래픽스 분야에서도 삼각함수는 핵심적인 역할을 합니다. 구체적인 사례는 다음과 같습니다:
- 3D 모델링: 3D 객체를 회전, 이동, 변형시킬 때 삼각함수를 사용하여 정확한 위치와 각도를 계산합니다.
- 애니메이션: 캐릭터나 객체의 움직임을 자연스럽게 구현하기 위해 삼각함수를 사용하여 위치와 각도를 조정합니다.
- 조명과 그림자: 장면에서 빛의 반사와 그림자의 위치를 계산할 때 삼각함수를 이용해 현실감 있는 그래픽을 구현합니다.

실생활에서 볼 수 있는 삼각함수의 대표적인 예는 무엇일까요?
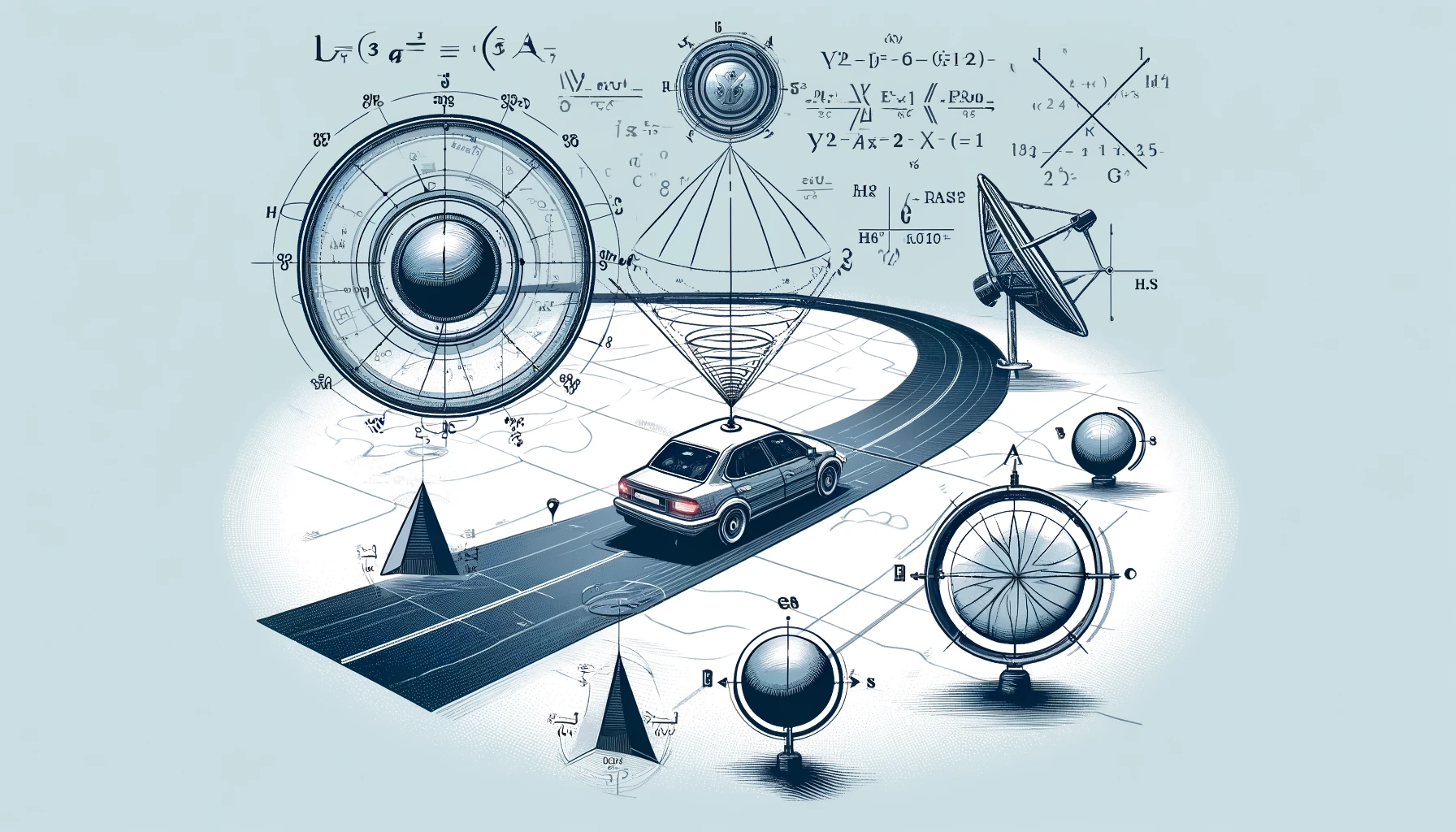
자동차 네비게이션 시스템의 작동 원리에도 삼각함수가 중요한 역할을 합니다. 구체적으로는 위성 위치 확인 시스템(GPS)에서 삼각함수가 사용됩니다. 자동차 네비게이션 시스템은 GPS 기술을 사용하여 차량의 위치를 파악하고, 최적의 경로를 계산합니다. 이를 위해 다음과 같은 원리가 적용됩니다.
1. GPS 위성과 삼각측량
GPS 시스템은 지구 궤도를 도는 여러 개의 인공위성을 사용합니다. 각 위성은 정확한 시간 신호를 지속적으로 송신합니다. 자동차의 GPS 수신기는 이 신호를 받아서 위성까지의 거리를 계산합니다. 이 거리를 계산하기 위해 삼각함수가 사용됩니다.
- 삼변측량(Trilateration): GPS 수신기는 최소 4개의 위성 신호를 받아야 정확한 위치를 계산할 수 있습니다. 각 위성으로부터의 거리 정보는 구의 형태로 나타나며, 이 구들이 교차하는 지점이 수신기의 위치를 나타냅니다. 삼각함수는 이 구들의 교차점을 계산하는 데 사용됩니다.
2. 거리 계산
위성 신호가 도달하는 시간을 기반으로 거리를 계산하는데, 이때 삼각함수가 필요합니다. GPS 신호는 빛의 속도로 이동하므로, 신호가 수신기에 도달하는 시간과 빛의 속도를 이용해 거리를 계산할 수 있습니다.
- 시간차와 거리: 신호가 위성에서 출발해 수신기에 도달하는 데 걸리는 시간을 측정하여 거리를 계산합니다. 이 거리는 d=c×td = c \times t (여기서 dd는 거리, cc는 빛의 속도, tt는 시간)로 구할 수 있습니다.
3. 위치 계산
각 위성으로부터의 거리 정보를 통해 자동차의 정확한 위치를 계산합니다. 이는 3차원 공간에서의 좌표를 구하는 문제로, 삼각함수와 선형 대수학이 결합되어 사용됩니다.
- 3차원 위치 계산: 여러 위성으로부터의 거리 데이터를 이용해 지구 좌표계에서 차량의 정확한 위치를 결정합니다. 이 과정에서 삼각함수는 필수적입니다.
4. 경로 최적화
네비게이션 시스템은 현재 위치에서 목적지까지의 최적 경로를 계산합니다. 이 과정에서도 삼각함수가 사용됩니다.
- 각도와 거리 계산: 두 지점 사이의 최단 경로를 계산하고, 방향을 설정하는 데 삼각함수가 사용됩니다. 이는 지도 상에서의 두 점 사이의 각도와 거리를 정확하게 계산하는 데 필요합니다.

결론
삼각함수는 우리의 일상생활과 다양한 산업에서 중요한 역할을 합니다. 건축과 토목 공학, 항공과 항해, 의료 영상, 물리학과 엔지니어링, 컴퓨터 그래픽스 등 많은 분야에서 삼각함수가 실질적인 문제 해결에 어떻게 활용되는지 알아보았습니다. 또한 천문학, 음악, 의료 분야 등에서 삼각함수의 중요성을 이해하고, 이를 통해 더욱 효율적으로 문제를 해결할 수 있습니다. 실생활 예시를 통해 삼각함수를 쉽게 이해하고 적용할 수 있기를 바랍니다.
'정보' 카테고리의 다른 글
| 최소공배수 구하는법: 간단하고 쉽게 배우는 방법 (0) | 2024.07.09 |
|---|---|
| 비평문 예시: 문학 작품과 영화 분석 (0) | 2024.07.03 |
| 김민재 바이에른 뮌헨 이적 아시아 최고 연봉 김민재 인스타그램 (0) | 2023.07.20 |
| 유튜브 다운로드, 유튜브 영상 다운로드 저장, 유튜브 음원 추출 방법 (0) | 2023.07.03 |
| MBTI ISFP 유형 특징, 성격, ISFP 유형 궁합, ISFP 장단점 (0) | 2023.06.26 |




댓글