정육면체 겉넓이 공식: 쉽게 이해하는 방법
정육면체란 무엇인가요?
정육면체는 모든 면이 동일한 정사각형으로 이루어진 3차원 도형입니다. 각 면이 크기와 모양이 같기 때문에, 그 구조를 이해하는 것이 겉넓이 계산의 첫걸음입니다. 정육면체는 총 6개의 면을 가지고 있으며, 모든 면은 동일한 크기를 가지고 있습니다.

정육면체의 겉넓이 공식
정육면체의 겉넓이를 구하는 공식은 매우 간단합니다. 먼저 정육면체의 한 변의 길이를 a라고 가정합니다. 그러면 정육면체의 각 면의 넓이는 정사각형의 넓이, 즉 a×a가 됩니다. 이렇게 동일한 면이 6개 있기 때문에, 이를 모두 더하면 정육면체의 겉넓이가 나옵니다.
공식:
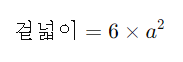
여기서 a는 정육면체의 한 변의 길이입니다.
예시:
만약 정육면체의 한 변의 길이가 4cm라면, 겉넓이는 다음과 같이 계산됩니다.
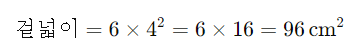
따라서 이 정육면체의 겉넓이는 96cm²가 됩니다.
정육면체 공식 이해하기
이 공식은 매우 직관적입니다. 정육면체는 총 6개의 정사각형 면으로 이루어져 있고, 각 면의 넓이는 a^2입니다. 따라서 이를 6배하면 전체 겉넓이를 구할 수 있습니다. 이 공식은 수학적 계산뿐만 아니라, 실제 생활에서도 적용될 수 있습니다. 예를 들어, 정육면체 모양의 상자나 큐브 형태의 물건들의 겉면을 계산할 때 유용합니다.
정육면체 겉넓이 공식 응용
정육면체 겉넓이 공식은 단순한 기하학적 계산에 그치지 않고, 다양한 실제 상황에서 응용할 수 있습니다. 예를 들어, 정육면체 모양의 상자를 만들 때 겉넓이를 계산하여 포장지나 재료의 양을 측정하는 데 활용할 수 있습니다.
또한, 이 공식은 수학 문제를 푸는 데 자주 사용됩니다. 특히 중학교나 고등학교 수학 문제에서 정육면체와 관련된 문제가 나오면 이 공식이 매우 유용하게 쓰입니다.
정리
정육면체의 겉넓이를 계산하는 공식은 매우 간단하고 직관적입니다. 공식은 6 × a^2로, 여기서 a는 정육면체의 한 변의 길이입니다. 이 공식을 통해 쉽게 정육면체의 겉넓이를 구할 수 있으며, 실제 생활에서도 여러 상황에서 응용할 수 있습니다.
'정보' 카테고리의 다른 글
| 비교우위 계산방법: 쉽게 이해하는 경제학의 핵심 개념 (5) | 2024.10.01 |
|---|---|
| 비교우위: 경제학의 핵심 개념 (0) | 2024.10.01 |
| 부채꼴 넓이 공식: 쉽게 이해하는 방법 (0) | 2024.09.25 |
| 교종과 선종의 차이: 불교의 두 갈래 (0) | 2024.09.14 |
| 시민 불복종의 사례와 철학적 배경 (0) | 2024.07.13 |




댓글