부채꼴 넓이 공식: 쉽게 이해하는 방법
부채꼴이란 무엇인가요?
부채꼴은 원의 일부분으로, 원의 중심에서 두 개의 반지름으로 나누어진 부분을 말합니다. 우리가 흔히 사용하는 '부채'의 모양과 비슷하기 때문에 '부채꼴'이라고 불리며, 기하학에서 중요한 도형 중 하나입니다.
부채꼴은 원의 중심각에 따라 넓이가 달라지며, 중심각이 커질수록 부채꼴의 넓이도 커집니다.

부채꼴 넓이 공식
부채꼴의 넓이를 구하는 공식은 다음과 같습니다. 부채꼴의 넓이는 원의 넓이와 중심각(라디안) 사이의 비율을 통해 계산됩니다.
부채꼴 넓이 공식:

여기서:
- r은 원의 반지름
- θ는 중심각 (라디안 단위)
중심각이 도 단위인 경우:

여기서 θ는 중심각의 크기 (도 단위)입니다.
예시: 부채꼴 넓이 계산하기
예시 1: 중심각이 라디안일 경우
반지름이 5cm이고 중심각이 π/3 라디안인 부채꼴의 넓이를 구해봅시다.

따라서 이 부채꼴의 넓이는 약 13.09cm²입니다.
예시 2: 중심각이 도 단위일 경우
반지름이 7cm이고 중심각이 60도인 부채꼴의 넓이를 구해보겠습니다.

따라서 이 부채꼴의 넓이는 약 25.66cm²입니다.
부채꼴 넓이 공식 유도 과정
부채꼴의 넓이는 원의 전체 넓이와 중심각 사이의 비율에 따라 결정됩니다. 원의 전체 넓이는 πr^2입니다. 부채꼴은 원의 일부분이므로, 전체 원의 넓이에 중심각이 원 전체의 몇 분의 몇인지를 곱하면 부채꼴의 넓이를 구할 수 있습니다.
예를 들어, 중심각이 θ 라디안인 부채꼴의 경우, 원 전체에서 이 부채꼴이 차지하는 비율은 θ/2π입니다. 따라서 전체 원의 넓이인 πr^2에 이 비율을 곱하면 부채꼴의 넓이가 나옵니다.
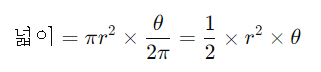
부채꼴 공식의 활용
부채꼴 넓이 공식은 여러 실제 상황에서 유용하게 쓰입니다. 예를 들어, 부채꼴 모양의 공원 설계, 부채꼴 모양의 구조물 계산, 또는 수학 문제 풀이 등에서 활용할 수 있습니다. 또한, 원을 분할하는 문제나 다양한 기하학 문제를 풀 때도 매우 유용한 공식입니다.
결론
부채꼴 넓이를 구하는 공식은 수학적으로 매우 간단합니다. 반지름 r과 중심각 θ를 알면 손쉽게 넓이를 계산할 수 있습니다. 중심각이 라디안 단위일 경우 1/2*r^2, 도 단위일 경우 πr^2 공식을 사용하여 계산할 수 있습니다.
이 공식을 통해 부채꼴의 넓이를 빠르고 정확하게 구할 수 있으며, 수학 문제뿐만 아니라 실제 생활에서도 유용하게 적용할 수 있습니다.
'정보' 카테고리의 다른 글
| 비교우위: 경제학의 핵심 개념 (0) | 2024.10.01 |
|---|---|
| 정육면체 겉넓이 공식: 쉽게 이해하는 방법 (1) | 2024.09.25 |
| 교종과 선종의 차이: 불교의 두 갈래 (0) | 2024.09.14 |
| 시민 불복종의 사례와 철학적 배경 (0) | 2024.07.13 |
| 직육면체 겉넓이 공식 완벽 정리: 예제와 함께 배우는 수학 (0) | 2024.07.10 |




댓글