세제곱 곱셈공식 완벽 설명: (a + b)³, (a - b)³ 공식부터 응용까지
수학에서 다항식을 다루다 보면 제곱뿐만 아니라 세제곱 공식도 반드시 배워야 합니다. 세제곱 공식은 중학교 후반~고등학교 초반 과정에서 처음 배우지만, 이때 제대로 이해하지 못하면 이후 수학에서 어려움을 겪게 됩니다. 오늘은 세제곱을 이용한 곱셈공식을 처음부터 끝까지 친절히 설명하겠습니다. 공식만 외우지 말고, 그 의미와 활용법까지 알아보세요!

세제곱 곱셈공식이란?
세제곱 공식은 말 그대로 어떤 수나 다항식의 세제곱(³)을 전개할 때 쓰이는 공식입니다. 제곱 공식이 (a + b)², (a - b)²로 나뉘는 것처럼, 세제곱 공식은 (a + b)³, (a - b)³로 나뉩니다.
제곱 공식과 다른 점은 전개 과정에서 항이 더 많아지고, 계산도 복잡해진다는 점입니다. 하지만 공식을 이해하면 복잡한 다항식도 빠르고 정확하게 계산할 수 있습니다.

세제곱 곱셈공식의 기본 형태
1️⃣ (a + b)³ 공식
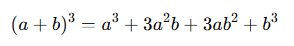
이 공식은 파스칼의 삼각형에서 1:3:3:1의 계수를 따릅니다. 각각 a³, a²b, ab², b³ 항이 들어가며, 중간의 두 항은 3배씩 등장합니다.
2️⃣ (a - b)³ 공식
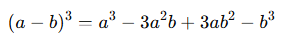
이 공식은 (a + b)³의 부호만 교체된 버전입니다. 중간 항의 부호에 주의하세요! 첫째, 셋째 항은 +, 둘째, 넷째 항은 -가 붙습니다.

3️⃣ a³ + b³ 공식
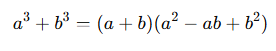
두 수의 세제곱의 합은 이처럼 인수분해할 수 있습니다.
4️⃣ a³ - b³ 공식
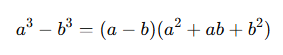
두 수의 세제곱의 차 역시 위와 같이 인수분해됩니다.

예제 풀이로 이해하기
예제 1: (2x + 3)³ 전개하기
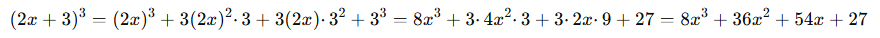
예제 2: (y - 5)³ 전개하기
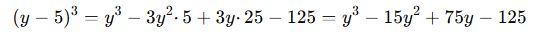

예제 3: a³ + b³ 인수분해
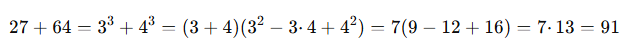
예제 4: a³ - b³ 인수분해
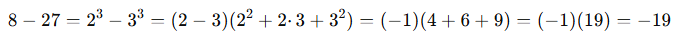
세제곱 곱셈공식의 활용법
세제곱 공식을 알면 단순히 전개나 인수분해 문제를 빠르게 풀 수 있을 뿐 아니라, 더 복잡한 함수 문제, 방정식 문제, 심지어 수학 경시대회 문제까지 접근할 수 있는 도구가 됩니다.
특히, 인수분해 공식
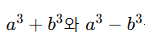
는 고등학교에서 많이 쓰이므로, 반드시 정확히 이해하고 외워야 합니다.
세제곱 곱셈공식 쉽게 외우는 방법
✅ 패턴 기억하기
- (a + b)³: 양 + 양 + 양 + 양 (모든 항 양수)
- (a - b)³: 양 - 양 + 양 - 양 (첫 항부터 번갈아 부호)
- a³ + b³, a³ - b³: 인수분해 형태로 묶어 외우기
✅ 직접 써보고 소리 내서 읽기
손으로 써보고, 소리 내어 읽으면 암기가 더 잘 됩니다.
✅ 예제 문제 풀어보기
공식만 외우면 금방 잊어버립니다. 실제 문제를 많이 풀면서 몸에 익히세요.

세제곱 공식의 확장
세제곱 공식은 멀리 보면 다항식 일반 전개로 확장됩니다. 고등학교에서는 이항정리(binomial theorem)를 배우는데, 이 역시 파스칼 삼각형 계수를 따르는 확장 공식입니다. (a + b)ⁿ을 전개하는 일반식까지 자연스럽게 연결되니, 세제곱 공식을 확실히 이해하면 이후 고급 수학에서도 탄탄한 기초가 됩니다.

수학 성적을 올리는 실질적 팁
공식만 달달 외우는 학생과, 공식을 실제 문제에 적용해 보는 학생은 성적에서 큰 차이가 납니다. 세제곱 곱셈공식을 배우면 곧바로 예제 문제를 풀어보고, 모르는 문제는 왜 틀렸는지 분석해 보세요. 공식을 안다고 끝이 아닙니다. '어디서, 어떻게 써야 하는지'까지 감각적으로 익히는 것이 중요합니다.

결론
세제곱 곱셈공식은 수학 공부의 필수 도구입니다. (a + b)³, (a - b)³ 전개 공식뿐 아니라 a³ + b³, a³ - b³ 인수분해 공식까지 정확히 외우고, 예제 문제를 풀어보며 실력을 다져 보세요. 이렇게 기초를 튼튼히 쌓아야 고난도 수학 문제도 겁먹지 않고 풀 수 있습니다.
오늘부터 곱셈공식을 문제에 적용하며 연습해 보세요. 수학 실력이 눈에 띄게 성장할 것입니다!
'정보' 카테고리의 다른 글
| 취학 전 자녀 학원비, 연말정산 교육비 공제 가능한가? (0) | 2025.05.22 |
|---|---|
| 곱셈공식 완전 정복: 중학생도 이해할 수 있는 수학 필수 공식 (0) | 2025.05.01 |
| 부피 구하는 공식 총정리: 직육면체, 원기둥, 구, 피라미드까지 완벽 정리 (1) | 2025.05.01 |
| 트롤리 딜레마란? 도덕적 판단을 시험하는 철학 실험 (1) | 2025.05.01 |
| 지렛대의 원리와 실생활 활용 사례 – 작은 힘으로 세상을 움직이다 (0) | 2025.05.01 |




댓글