부피 구하는 공식 총정리: 직육면체, 원기둥, 구, 피라미드까지 완벽 정리
수학과 과학에서 공간을 다룰 때 가장 중요한 개념 중 하나가 바로 부피입니다. 부피는 3차원 공간에서 어떤 물체가 차지하는 공간의 크기를 의미하며, 실생활에서도 박스 포장, 물의 양 측정, 공사 재료 계산 등 여러 상황에서 필요합니다. 오늘 이 글에서는 각 도형의 부피 구하는 공식을 한 번에 정리해 드리겠습니다.
공식만 나열하지 않고, 각 공식의 의미와 예시, 활용법까지 설명할 테니 끝까지 읽어 보세요!

부피란 무엇인가?
부피는 3차원 물체가 차지하는 공간의 크기입니다. 2차원 도형은 넓이로 크기를 측정하지만, 3차원 도형은 길이 × 넓이 × 높이 같은 계산을 통해 입체적으로 크기를 측정합니다.
부피의 단위는 보통 cm³, m³, L(리터), mL(밀리리터) 등으로 표현되며, 주어진 단위를 잘 맞춰 계산하는 것도 중요합니다.

기본적인 부피 구하는 공식
1. 직육면체 부피
부피 = 가로 × 세로 × 높이
예: 가로 4cm, 세로 3cm, 높이 2cm인 박스의 부피는
4 × 3 × 2 = 24 cm³
직육면체는 가장 기본적인 입체도형으로, 공책, 상자, 책 등 실생활에서 매우 자주 등장합니다.

2. 정육면체 부피
부피 = 한 변의 길이 × 한 변의 길이 × 한 변의 길이 = 한 변의 길이³
예: 한 변의 길이가 5cm인 정육면체의 부피는
5 × 5 × 5 = 125 cm³
정육면체는 모든 면이 같은 정사각형인 큐브 모양입니다. 예를 들어 주사위, 루빅스 큐브 등이 여기에 해당합니다.

3. 원기둥 부피
부피 = 밑넓이 × 높이 = π × 반지름² × 높이
예: 반지름 3cm, 높이 10cm인 원기둥의 부피는
π × 3 × 3 × 10 = π × 9 × 10 = 90π ≈ 282.74 cm³
원기둥은 캔, 컵, 파이프 등에서 자주 볼 수 있는 모양입니다.

4. 원뿔 부피
부피 = (1 ÷ 3) × 밑넓이 × 높이 = (1 ÷ 3) × π × 반지름² × 높이
예: 반지름 4cm, 높이 9cm인 원뿔의 부피는
(1 ÷ 3) × π × 4 × 4 × 9 = (1 ÷ 3) × π × 16 × 9 = (1 ÷ 3) × 144π = 48π ≈ 150.8 cm³
원뿔은 아이스크림 콘, 원뿔형 종이컵 등에서 볼 수 있습니다.

5. 구의 부피
부피 = (4 ÷ 3) × π × 반지름³
예: 반지름 5cm인 구의 부피는
(4 ÷ 3) × π × 5 × 5 × 5 = (4 ÷ 3) × π × 125 = 약 523.6 cm³
구는 공, 물방울, 구슬 등에서 볼 수 있습니다.

6. 피라미드 부피
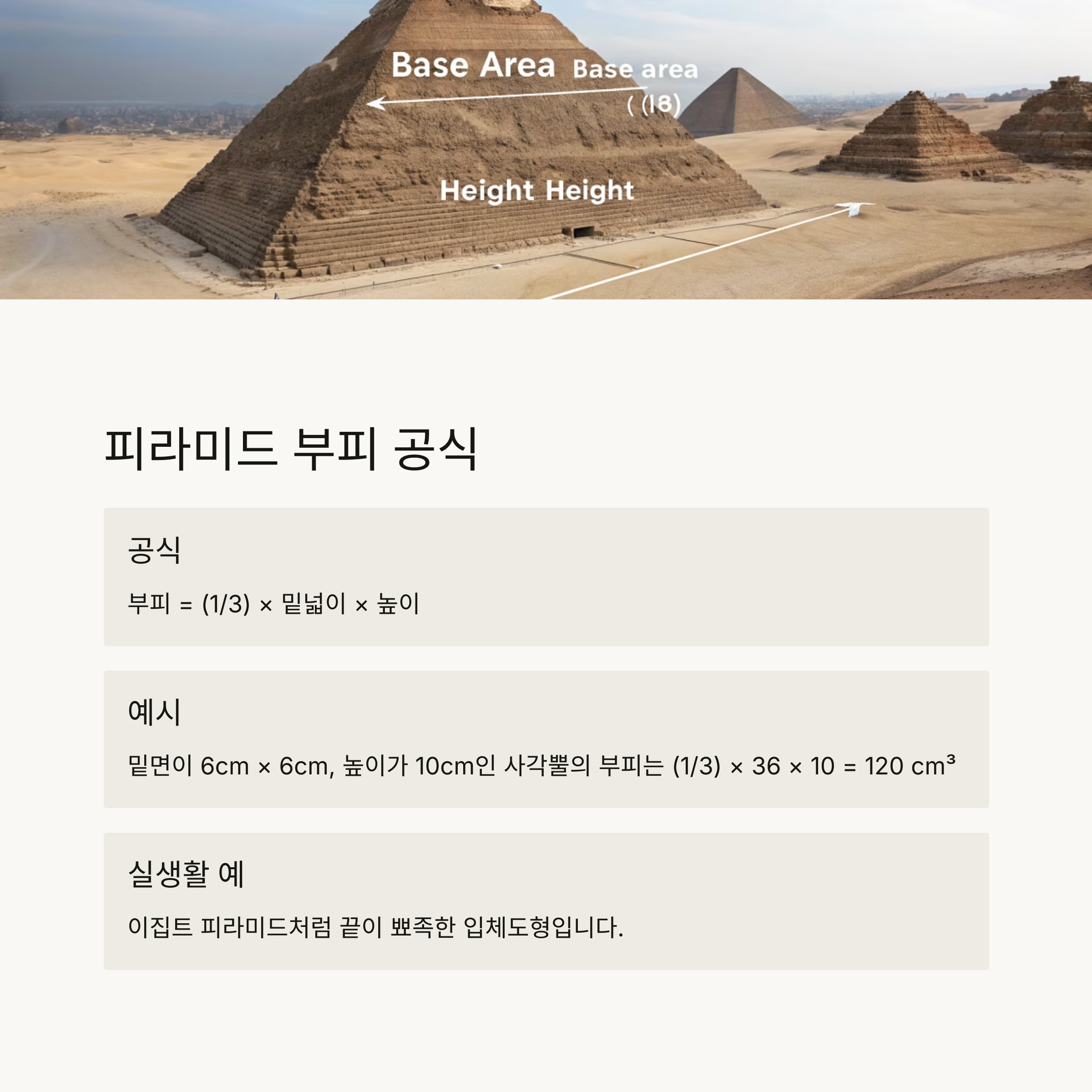
부피 = (1 ÷ 3) × 밑넓이 × 높이
예: 밑면이 6cm × 6cm, 높이가 10cm인 사각뿔의 부피는
(1 ÷ 3) × (6 × 6) × 10 = (1 ÷ 3) × 36 × 10 = (1 ÷ 3) × 360 = 120 cm³
피라미드는 이집트 피라미드처럼 끝이 뾰족한 입체도형입니다.
실생활 속 부피 계산 예시
물통의 물 용량 구하기
직육면체 모양 물통(가로 20cm, 세로 10cm, 높이 30cm)의 최대 용량은
20 × 10 × 30 = 6000 cm³ = 6L
공의 부피 구하기
반지름 7cm인 축구공의 부피는
(4 ÷ 3) × π × 7 × 7 × 7 ≈ 약 1436.8 cm³
파이프 부피 구하기
내부 반지름 5cm, 길이 200cm(2m)인 파이프의 부피는
π × 5 × 5 × 200 = π × 25 × 200 = 5000π ≈ 15,707.96 cm³

부피 계산 시 주의할 점
단위를 통일할 것
cm, m, mm 단위가 섞여 있으면 반드시 하나로 맞춰야 합니다. 예를 들어, m는 cm로 바꿔서 계산하세요.
밑넓이를 정확히 구할 것
원뿔, 원기둥, 피라미드는 밑넓이가 중요합니다. 밑넓이가 무엇인지 문제에서 정확히 파악하세요.
π 값 주의
문제에서 요구하는 대로 π는 3.14로 계산하거나, π 그대로 두어야 합니다.

부피 공식을 쉽게 외우는 방법
그림 그리기
각 도형의 밑넓이, 높이를 눈으로 보고 표시해 보세요.
짧은 암기 문장 만들기
- 직육면체: 가세높
- 원기둥: 파이 알제곱 높이
- 원뿔, 피라미드: 삼분의일 밑넓이 높이
- 구: 사분의삼 파이 알세제곱
집에서 실생활 예제로 연습
상자, 컵, 공을 측정해 실제 부피를 계산해 보면 훨씬 기억에 남습니다.

결론
부피 구하는 공식은 수학 문제에서만 쓰이는 것이 아닙니다. 물건의 용량, 공간의 크기, 건축 재료 양 등 다양한 분야에서 실제로 사용됩니다. 각 도형의 특징과 공식을 잘 외워 두고 문제에 적용해 보세요. 부피 계산에 능숙해지면 수학 실력은 물론, 실생활에서 필요한 계산 능력도 높아집니다.

'정보' 카테고리의 다른 글
| 곱셈공식 완전 정복: 중학생도 이해할 수 있는 수학 필수 공식 (0) | 2025.05.01 |
|---|---|
| 세제곱 곱셈공식 완벽 설명: (a + b)³, (a - b)³ 공식부터 응용까지 (0) | 2025.05.01 |
| 트롤리 딜레마란? 도덕적 판단을 시험하는 철학 실험 (1) | 2025.05.01 |
| 지렛대의 원리와 실생활 활용 사례 – 작은 힘으로 세상을 움직이다 (0) | 2025.05.01 |
| 고교학점제 도입과 2028 대입 개편 – 학생과 학부모가 꼭 알아야 할 변화 (0) | 2025.02.21 |




댓글