수학 내분점 공식 완벽 가이드: 쉽게 이해하는 방법
내분점 공식은 두 점 사이의 특정 비율에 따라 점을 나누는 위치를 찾는 데 사용되는 수학 공식입니다. 좌표 평면에서 중요한 역할을 하며, 기하학적 문제를 해결하는 데 유용합니다. 내분점 공식은 선분을 일정한 비율로 나누는 점의 좌표를 구하는 데 사용되며, 내분점과 외분점으로 나눌 수 있습니다. 이 공식의 이해는 수학적 문제 해결에 큰 도움이 되며, 좌표 평면의 기초를 다지는 데 중요한 역할을 합니다. 이 글에서는 내분점 공식의 기본 원리와 활용 방법, 예제와 함께 자세히 알아보겠습니다.

1. 내분점 공식이란?
내분점 공식은 두 점 사이의 특정 비율에 따라 점을 나누는 위치를 찾는 데 사용되는 수학 공식입니다. 좌표 평면에서 중요한 역할을 하며, 기하학적 문제를 해결하는 데 유용합니다.
P(x, y) = ((mx2 + nx1) / (m + n), (my2 + ny1) / (m + n))
내분점 공식은 두 점 A(x1,y1)와 B(x2,y2)를 연결하는 선분을 m:의 비율로 나누는 점 P(x,y)의 좌표를 구하는 공식입니다. 내분점 공식을 사용하면 다음과 같이 점 P의 좌표를 구할 수 있습니다.
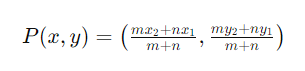
여기서 과 은 두 점 A와 B 사이의 거리 비율을 나타냅니다.
2. 내분점 공식의 유도 과정
내분점 공식은 선분을 일정한 비율로 나누는 점의 좌표를 구하는 데 사용됩니다. 두 점 A(x1, y1)과 B(x2, y2)가 있을 때, 이 선분을 m:n 비율로 나누는 점 P의 좌표는 다음과 같이 구할 수 있습니다:
P(x, y) = ((mx2 + nx1) / (m + n), (my2 + ny1) / (m + n))

3. 내분점 공식의 활용 방법
3-1. 내분점 예제 풀이
점 A(2, 3)과 점 B(8, 7)를 3:2의 비율로 나누는 점 P의 좌표를 구해봅시다.
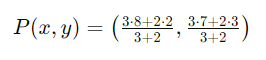
이제 이 공식을 하나씩 풀어볼겠습니다.
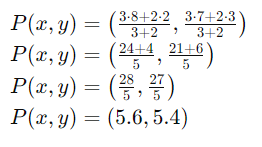
따라서, 점 P의 좌표는 (5.6, 5.4)입니다.
3-2. 외분점 예제 풀이
외분점 공식은 두 점을 특정 비율로 외분하는 점을 구하는 공식입니다.
외분점 공식은 두 점 A(x1, y1)과 B(x2, y2)가 있을 때, 이 선분을 m:n 비율로 외분하는 점 P의 좌표를 다음과 같이 구할 수 있습니다.
P(x, y) = ((mx2 - nx1) / (m - n), (my2 - ny1) / (m - n))
예를 들어, 점 A(1, 2)와 B(4, 6)을 3:1 비율로 외분하는 점 Q의 좌표는 다음과 같습니다:
Q(x, y) = ((3*4 - 1*1) / (3 - 1), (3*6 - 1*2) / (3 - 1))
= (12 - 1) / 2, (18 - 2) / 2
= 11 / 2, 16 / 2
= (5.5, 8)
따라서, 점 Q의 좌표는 (5.5, 8)입니다.
4. 내분점 공식의 중요성
내분점 공식은 기하학적 문제 해결에 필수적인 도구입니다. 특히, 좌표 평면에서의 문제 해결과 그래프를 이해하는 데 중요한 역할을 합니다. 이 공식은 수학적 사고를 확장시키고 문제 해결 능력을 향상시키는 데 큰 도움이 됩니다.
5. 내분점 공식을 활용한 문제 해결
내분점 공식을 활용하면 다양한 기하학적 문제를 해결할 수 있습니다. 예를 들어, 삼각형의 무게 중심을 구하거나, 선분을 일정한 비율로 나누는 점을 찾는 문제 등에서 유용하게 사용됩니다.
또한 내분점 공식은 지도에서 위치를 찾거나, 디자인에서 특정 지점을 나누는 등 다양한 실생활 문제에 적용할 수 있습니다. 예를 들어, 두 도시 A와 B 사이의 거리를 일정한 비율로 나눠 중간 지점을 찾을 때 활용할 수 있습니다.
내분점 공식의 활용
- 기하학 문제 해결: 기하학적 도형의 특정 점을 찾는 데 유용합니다.
- 컴퓨터 그래픽스: 화면에서 객체의 위치를 계산할 때 사용됩니다.
- 물리학: 물체의 무게 중심을 구할 때 활용할 수 있습니다.
6. 결론
내분점 공식이란?
내분점 공식은 선분을 일정한 비율로 나누는 점의 좌표를 구하는 데 사용됩니다. 두 점 A(x1, y1)과 B(x2, y2)가 있을 때, 이 선분을 m:n 비율로 나누는 점 P의 좌표는 다음과 같이 구할 수 있습니다.
| 내분점 공식 | P(x, y) = ((mx2 + nx1) / (m + n), (my2 + ny1) / (m + n)) |
내분점 공식은 수학에서 매우 중요한 개념입니다. 이 공식의 이해와 활용은 좌표 평면에서의 문제 해결에 큰 도움을 주며, 기하학적 사고를 확장시키는 데 기여합니다. 다양한 예제를 통해 내분점 공식을 이해하고 연습하면 수학적 문제 해결 능력을 크게 향상시킬 수 있습니다.
'교육 자료' 카테고리의 다른 글
| 쎈 3-2 답지 (2024년), 쎈 중등 수학 교재 소개 및 리뷰 (0) | 2024.07.11 |
|---|---|
| 백발백중 영어 중3-1 기말 답지 (능률 김성곤) (0) | 2024.06.30 |
| 백발백중 영어 중2-1 기말 답지 (능률 김성곤) (0) | 2024.06.10 |
| 백발백중 영어 중2-1 기말 답지 (동아 이병민) (0) | 2024.06.03 |
| 백발백중 영어 중2-1 기말 답지 (동아 윤정미) (0) | 2024.06.03 |




댓글